Learn Statistics

►統計は、実験データや実際の研究の特定のセットのために定量化されたモデル、表現やあらすじを使用して数学的分析の一形態です。統計学の方法論は、収集見直し、分析し、データから結論を引き出すこと。いくつかの統計的な対策は平均、回帰分析、歪度、尖度、分散とvariance.✦の分析が含まれます

  【このアプリの中で取り上げるトピックは以下のとおりです】

⇢調整R-乗

分散分析⇢

⇢算術平均

⇢算術中央値

⇢演算モード

⇢算術レンジ

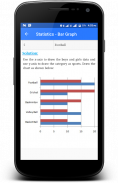
バーグラフ⇢

ベストポイント推定⇢

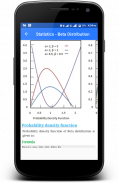
⇢ベータ分布

⇢二項分布

⇢ブラック - ショールズ方程式

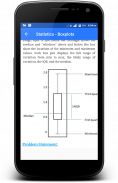
⇢ボックスプロット

⇢中心極限定理

⇢チェビシェフの定理

⇢カイ二乗分布

⇢カイ二乗テーブル

⇢円順列

⇢クラスターサンプリング

⇢Cohenのカッパ係数

⇢コンビネーション

交換と⇢コンビネーション

⇢プロットを比較すると、

⇢継続的な一様分布

⇢累積頻度

⇢変動の共同効率的

⇢相関共同効率的

⇢累積プロット

⇢累積ポアソン分布

⇢データ収集

⇢アンケートの設計

⇢観察

ケーススタディメソッド⇢

⇢データパターン

⇢十分位数統計

⇢ドットプロット

⇢指数分布

⇢F分布

⇢Fテストテーブル

⇢階乗

⇢頻度分布

⇢ガンマ分布

⇢幾何平均

⇢幾何確率分布

⇢フィットの良さ

⇢グランド平均

⇢ガンベル分布

調和平均⇢

⇢ハーモニック数

⇢高調波共振周波数

⇢ヒストグラム

⇢超幾何分布

⇢区間推定

逆ガンマ分布⇢

⇢コルモゴロフスミルノフテスト

⇢尖度

ラプラス分布⇢

⇢線形回帰

⇢ログガンマ分布

⇢ロジスティック回帰

⇢マクネマーテスト

⇢平均偏差

⇢差を意味

⇢多項分布

⇢負の二項分布

⇢ポアソン分布

⇢パワー・カリキュレータ

⇢確率

⇢確率添加剤の定理

⇢確率乗法定理

⇢確率ベイズの定理

⇢確率密度関数

⇢プロセス能力（CP）＆プロセス性能（PP）

⇢プロセスシグマ

⇢二次回帰式

⇢定性的データ対定量的データ

⇢四分位偏差

親指の⇢範囲ルール

⇢レイリー分布

⇢回帰インターセプト信頼区間

⇢相対標準偏差

⇢信頼性係数

⇢必要なサンプルサイズ

⇢残留分析

正方形の⇢残留和

⇢二乗平均平方根

⇢サンプル計画

⇢サンプリング方法

⇢散布

⇢シャノンウィーナー多様性指数

⇢シグナル対ノイズ比

⇢シンプルランダムサンプリング

⇢歪度

⇢標準偏差

⇢標準誤差（SE）

⇢標準正常テーブル

⇢統計的意義

⇢式

⇢表記

⇢茎と葉のプロット

⇢層化抽出

⇢学生Tテスト

広場の⇢和

⇢t分布表

⇢のTi 83指数回帰

⇢変換

⇢Trimmed平均値

⇢タイプI＆IIのエラー

⇢分散

⇢ベン図

大数の法則⇢弱いです

⇢Zテーブル